from IPython.core.display import display, HTML
display(HTML("<style> .container{width:90% !important;}</style>"))
1. 앙상블 학습이란?¶
앙상블(Ensemble) 학습¶
앙상블이란 여러 개의 알고리즘을 사용하여, 그 예측을 결함함으로써 보다 정확한 예측을 도출하는 기법을 말합니다.
집단지성이 힘을 발휘하는 것처럼 단일의 강한 알고리즘보다 복수의 약한 알고리즘이 더 뛰어날 수 있다는 생각에 기반을 두고 있습니다.
이미지, 영상, 음성 등의 비정형 데이터의 분류는 딥러닝이 뛰어난 성능을 보이지만,
대부분 정형 데이터의 분류에서는 앙상블이 뛰어난 성능을 보이고 있다고 합니다.
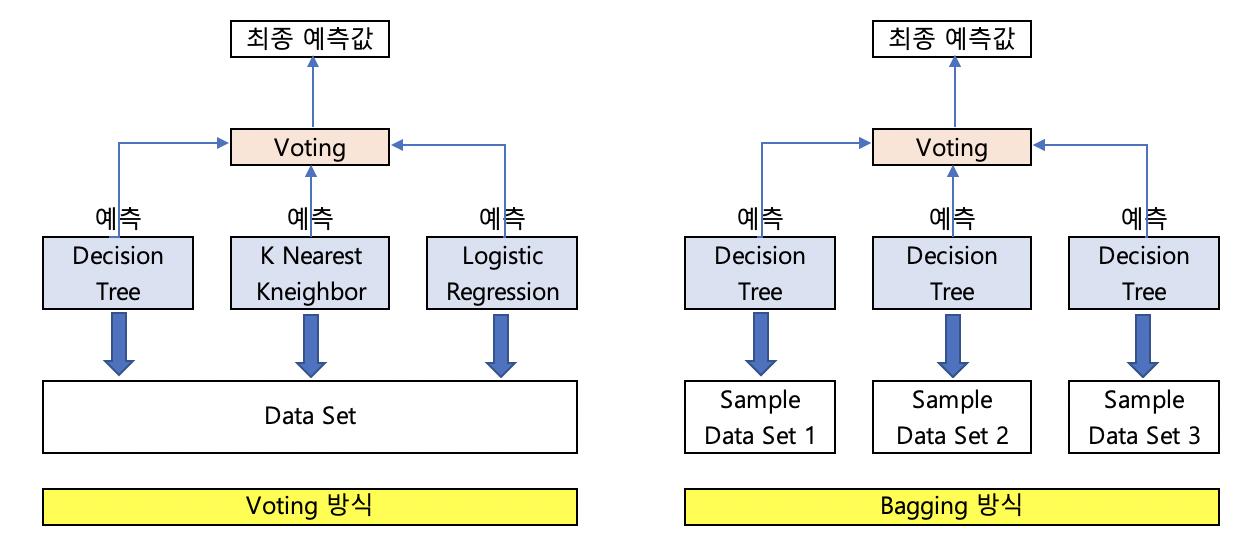
앙상블 학습의 유형은 보팅(Voting), 배깅(Bagging), 부스팅(Boosting), 스태킹(Stacking) 등이 있습니다.
보팅은 여러 종류의 알고리즘을 사용한 각각의 결과에 대해 투표를 통해 최종 결과를 예측하는 방식입니다.
배깅은 같은 알고리즘에 대해 데이터 샘플을 다르게 두고 학습을 수행해 보팅을 수행하는 방식입니다.
이 때의 데이터 샘플은 중첩이 허용됩니다. 즉 10000개의 데이터에 대해 10개의 알고리즘이 배깅을 사용할 때,
각 1000개의 데이터 내에는 중복된 데이터가 존재할 수 있습니다.
배깅의 대표적인 방식이 Random Forest 입니다.
부스팅은 여러 개의 알고리즘이 순차적으로 학습을 하되, 앞에 학습한 알고리즘 예측이 틀린 데이터에 대해
올바르게 예측할 수 있도록, 그 다음번 알고리즘에 가중치를 부여하여 학습과 예측을 진행하는 방식입니다.
마지막으로 스태킹은 여러 가지 다른 모델의 예측 결과값을 다시 학습 데이터로 만들어 다른 모델(메타 모델)로
재학습시켜 결과를 예측하는 방법입니다.
2. 하드보팅(Hard Voting)과 소프트보팅(Soft Voting)¶
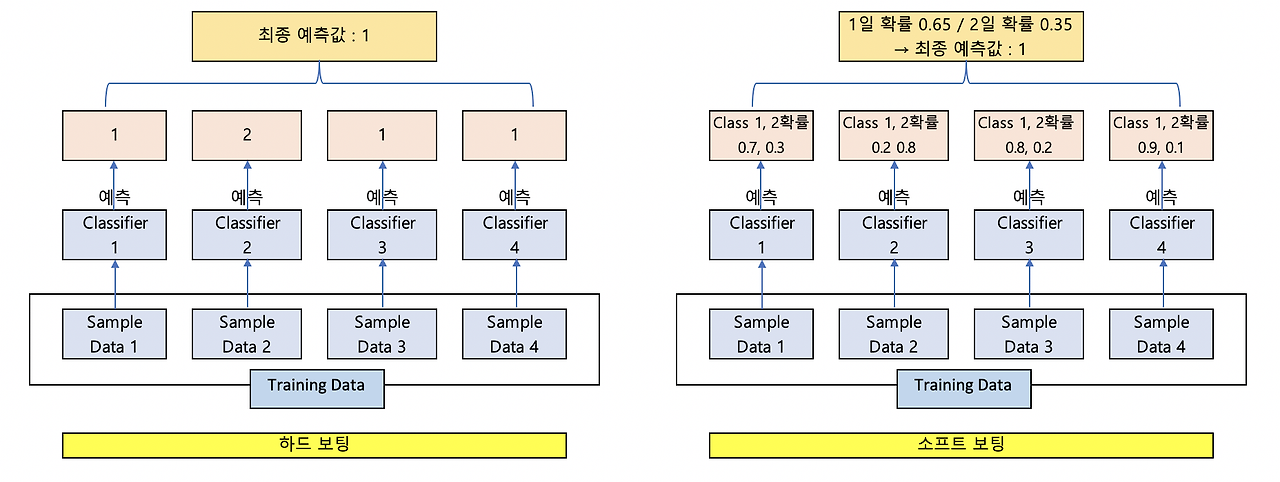
하드보팅을 이용한 분류는 다수결 원칙과 비슷합니다.
소프트 보팅은 각 알고리즘이 레이블 값 결정 확률을 예측해서, 이것을 평균하여 이들 중 확률이 가장 높은 레이블 값을 최종 값으로 예측합니다.
일반적으로는 소프트 보팅이 성능이 더 좋아서 많이 적용됩니다.
3. 보팅 분류기(Voting Classifier)¶
사이킷런은 보팅방식의 앙상블을 구현한 VotingClassifier 클래스를 제공하고 있습니다.
사이킷런에서 제공되는 위스콘신 유방암 데이터 세트를 이용해 보팅방식의 앙상블을 적용해보겠습니다.
# 필요한 모듈과 데이터 불러오기
import pandas as pd
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from warnings import filterwarnings
filterwarnings('ignore')
cancer = load_breast_cancer()
data_df = pd.DataFrame(cancer.data, columns = cancer.feature_names)
data_df.head(3)
로지스틱회귀와 KNN을 기반으로 하여 소프트 보팅 방식으로 보팅 분류기를 만들어 보겠습니다.
# 보팅 적용을 위한 개별 모델은 로지스틱 회귀와 KNN입니다.
logistic_regression = LogisticRegression()
knn = KNeighborsClassifier(n_neighbors=8)
# 개별모델을 소프트보팅 기반의 앙상블 모델로 구현한 분류기
voting_model = VotingClassifier(estimators=[ ('LogisticRegression', logistic_regression), ('KNN', knn)], voting='soft')
# 데이터를 훈련셋과 테스트셋으로 나누기
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, test_size=0.2, random_state=156)
# 보팅 분류기의 학습/예측/평가
voting_model.fit(X_train, y_train)
pred = voting_model.predict(X_test)
print('보팅 분류기의 정확도: {0: .4f}'.format(accuracy_score(y_test, pred)))
# 개별 모델의 학습/예측/평가
classifiers = [logistic_regression, knn]
for classifier in classifiers:
classifier.fit(X_train, y_train)
pred = classifier.predict(X_test)
class_name = classifier.__class__.__name__
print('{0} 정확도: {1:.4f}'.format(class_name, accuracy_score(y_test, pred)))
보팅 분류기의 정확도가 각 개별 모델의 정확도보다 조금 높게 나타났습니다.
하지만 여러 알고리즘을 결합한다고 항상 성능이 향상되는 것은 아닙니다.
'Machine Learning > 파이썬 머신러닝 완벽가이드 학습' 카테고리의 다른 글
| [Chapter 4. 분류] 부스팅알고리즘(AdaBoost, GBM) (0) | 2019.10.20 |
|---|---|
| [Chapter 4. 분류] 랜덤포레스트(Random Forest) (1) | 2019.10.19 |
| [Chapter 4. 분류] Decision Tree Classifier (0) | 2019.10.03 |
| [Chapter 3. 평가] 피마 인디언 당뇨병 데이터셋을 통한 평가지표 실습 (0) | 2019.10.03 |
| [Chapter 3. 평가] 머신러닝 성능 평가에 활용되는 지표들 (0) | 2019.10.02 |
