from IPython.core.display import display, HTML
display(HTML("<style> .container{width:90% !important;}</style>"))
1. 배깅(Bagging)이란?¶
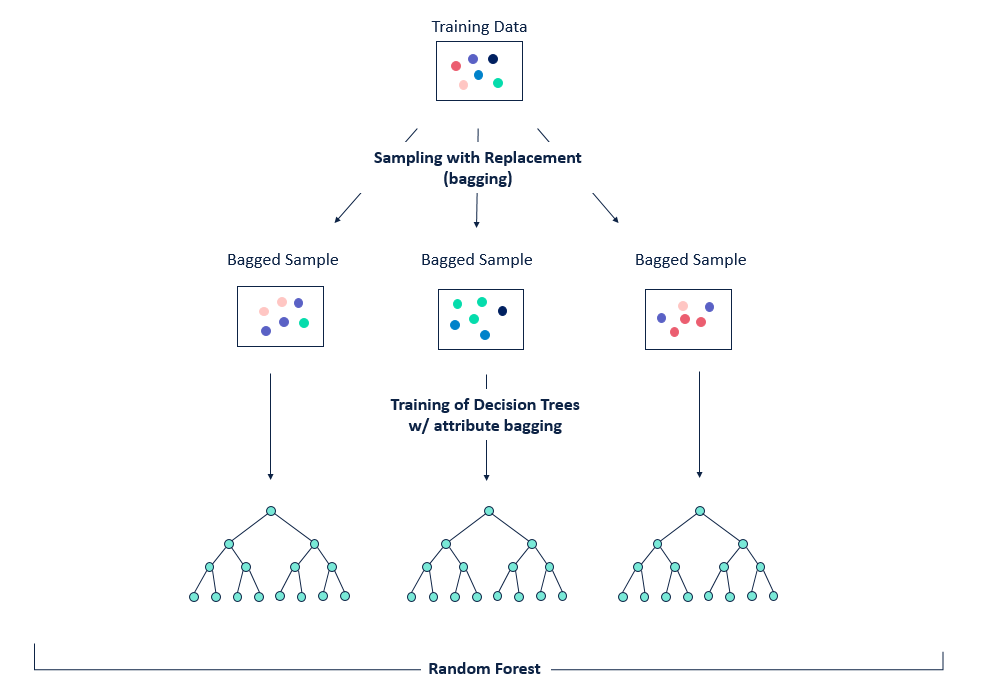
배깅(Bagging)은 Bootstrap Aggregating의 약자로, 보팅(Voting)과는 달리 동일한 알고리즘으로 여러 분류기를 만들어 보팅으로 최종 결정하는 알고리즘
**배깅은 다음과 같은 방식으로 진행이 됩니다.
(1) 동일한 알고리즘을 사용하는 일정 수의 분류기 생성
(2)각각의 분류기는 부트스트래핑(Bootstrapping)방식으로 생성된 샘플데이터를 학습
(3)최종적으로 모든 분류기가 보팅을 통헤 예측 결정
※ 부트스트래핑 샘플링은 전체 데이터에서 일부 데이터의 중첩을 허용하는 방식

2. 랜덤포레스트(RandomForest)¶
사용자 행동 데이터 세트를 이용한 RandomForest 예측¶
import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
import warnings
warnings.filterwarnings('ignore')
# 데이터셋을 구성하는 함수 설정
def get_human_dataset():
# 각 데이터 파일들은 공백으로 분리되어 있으므로 read_csv에서 공백문자를 sep으로 할당
feature_name_df = pd.read_csv('human_activity/features.txt', sep='\s+',
header=None, names=['column_index', 'column_name'])
# 데이터프레임에 피처명을 컬럼으로 뷰여하기 위해 리스트 객체로 다시 반환
feature_name = feature_name_df.iloc[:, 1].values.tolist()
# 학습 피처 데이터세트와 테스트 피처 데이터를 데이터프레임으로 로딩
# 컬럼명은 feature_name 적용
X_train = pd.read_csv('human_activity/train/X_train.txt', sep='\s+', names=feature_name)
X_test = pd.read_csv('human_activity/test/X_test.txt', sep='\s+', names=feature_name)
# 학습 레이블과 테스트 레이블 데이터를 데이터 프레임으로 로딩, 컬럼명은 action으로 부여
y_train = pd.read_csv('human_activity/train/y_train.txt', sep='\s+', names=['action'])
y_test = pd.read_csv('human_activity/test/y_test.txt', sep='\s+', names=['action'])
# 로드된 학습/테스트용 데이터프레임을 모두 반환
return X_train, X_test, y_train, y_test
# 학습/테스트용 데이터 프레임 반환
X_train, X_test, y_train, y_test = get_human_dataset()
# 랜덤 포레스트 학습 및 별도의 테스트 세트로 예측 성능 평가
rf_clf = RandomForestClassifier(random_state=0)
rf_clf.fit(X_train, y_train)
pred = rf_clf.predict(X_test)
accuracy = accuracy_score(y_test, pred)
print('랜덤 포레스트 정확도: {:.4f}'.format(accuracy))
3. 랜덤포레스트 하이퍼 파라미터 튜닝¶
랜덤포레스트는 트리기반의 하이퍼 파라미터에 배깅, 부스팅, 학습, 정규화 등을 위한 하이퍼 파라미터까지 추가되므로 튜닝할 파라미터가 많습니다.
| 파라미터 명 | 설명 |
|---|---|
| n_estimators | - 결정트리의 갯수를 지정 - Default = 10 - 무작정 트리 갯수를 늘리면 성능 좋아지는 것 대비 시간이 걸릴 수 있음 |
| min_samples_split | - 노드를 분할하기 위한 최소한의 샘플 데이터수 → 과적합을 제어하는데 사용 - Default = 2 → 작게 설정할 수록 분할 노드가 많아져 과적합 가능성 증가 |
| min_samples_leaf | - 리프노드가 되기 위해 필요한 최소한의 샘플 데이터수 - min_samples_split과 함께 과적합 제어 용도 - 불균형 데이터의 경우 특정 클래스의 데이터가 극도로 작을 수 있으므로 작게 설정 필요 |
| max_features | - 최적의 분할을 위해 고려할 최대 feature 개수 - Default = 'auto' (결정트리에서는 default가 none이었음) - int형으로 지정 →피처 갯수 / float형으로 지정 →비중 - sqrt 또는 auto : 전체 피처 중 √(피처개수) 만큼 선정 - log : 전체 피처 중 log2(전체 피처 개수) 만큼 선정 |
| max_depth | - 트리의 최대 깊이 - default = None → 완벽하게 클래스 값이 결정될 때 까지 분할 또는 데이터 개수가 min_samples_split보다 작아질 때까지 분할 - 깊이가 깊어지면 과적합될 수 있으므로 적절히 제어 필요 |
| max_leaf_nodes | 리프노드의 최대 개수 |
# RandomForest의 하이퍼 파라미터 default 상태
model = RandomForestClassifier()
model
GridSearchCV를 통한 랜덤포레스트의 하이퍼 파라미터 튜닝¶
from sklearn.model_selection import GridSearchCV
params = { 'n_estimators' : [10, 100],
'max_depth' : [6, 8, 10, 12],
'min_samples_leaf' : [8, 12, 18],
'min_samples_split' : [8, 16, 20]
}
# RandomForestClassifier 객체 생성 후 GridSearchCV 수행
rf_clf = RandomForestClassifier(random_state = 0, n_jobs = -1)
grid_cv = GridSearchCV(rf_clf, param_grid = params, cv = 3, n_jobs = -1)
grid_cv.fit(X_train, y_train)
print('최적 하이퍼 파라미터: ', grid_cv.best_params_)
print('최고 예측 정확도: {:.4f}'.format(grid_cv.best_score_))
#위의 결과로 나온 최적 하이퍼 파라미터로 다시 모델을 학습하여 테스트 세트 데이터에서 예측 성능을 측정
rf_clf1 = RandomForestClassifier(n_estimators = 100,
max_depth = 12,
min_samples_leaf = 8,
min_samples_split = 8,
random_state = 0,
n_jobs = -1)
rf_clf1.fit(X_train, y_train)
pred = rf_clf1.predict(X_test)
print('예측 정확도: {:.4f}'.format(accuracy_score(y_test,pred)))
Random Forest의 각 피처의 중요도 시각화 : featureimportances¶
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
ftr_importances_values = rf_clf1.feature_importances_
ftr_importances = pd.Series(ftr_importances_values, index = X_train.columns)
ftr_top20 = ftr_importances.sort_values(ascending=False)[:20]
plt.figure(figsize=(8,6))
plt.title('Top 20 Feature Importances')
sns.barplot(x=ftr_top20, y=ftr_top20.index)
plt.show()
'Machine Learning > 파이썬 머신러닝 완벽가이드 학습' 카테고리의 다른 글
| [Chapter 4. 분류] XGBoost(eXtraGradient Boost) (3) | 2019.10.27 |
|---|---|
| [Chapter 4. 분류] 부스팅알고리즘(AdaBoost, GBM) (0) | 2019.10.20 |
| [Chapter 4. 분류] 앙상블 학습 (0) | 2019.10.14 |
| [Chapter 4. 분류] Decision Tree Classifier (0) | 2019.10.03 |
| [Chapter 3. 평가] 피마 인디언 당뇨병 데이터셋을 통한 평가지표 실습 (0) | 2019.10.03 |