단일 층의 퍼셉트론을 넘어 여러 층의 퍼셉트론을 만들어 한 층의 출력을 다음 층으로 보낸다면 더욱 강력한 모델이 될 수 있음.
다만 활성함수가 선형의 함수라면 결국 이 여러 층도 한 개층으로 압축될 수가 있어 여러 층을 만드는 의미가 없음.
이 때문에 시그모이드, Relu 등과 같은 비선형 함수가 필요함.

여러 계층으로 만들었을 경우에도, 단일 계층에서처럼 입력, 가중치 합계, 활성화 기능 및 출력이 있음.
단일 계층일 때와의 차이는 아래와 같음
1) 이전 계층의 출력값을 입력값으로 받음
2) 활성함수로 비선형함수가 사용됨
3) 입력과 출력 사이에 추가된 계층(Hidden Layer)가 존재함
4) 뉴런 간 연결시 벡터가 아니라 매트릭스 형태로 연결이 됨
- 처음 입력 시 4 X 2 행렬로 가중치 합계 계산을 하고 Hidden Layer에서는 2 x 1 행렬로 계산을 함
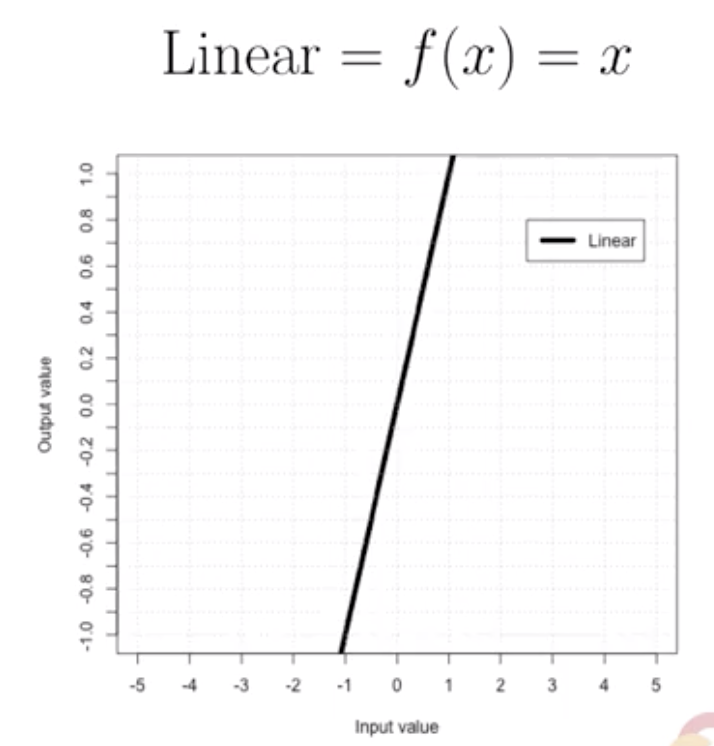
위와 같은 선형 활성함수를 사용시에는 최종 결과가 결국 입력 값과 어떤 상수의 조합으로 귀결됨.
이것은 결국 선형회귀에 지나지 않음
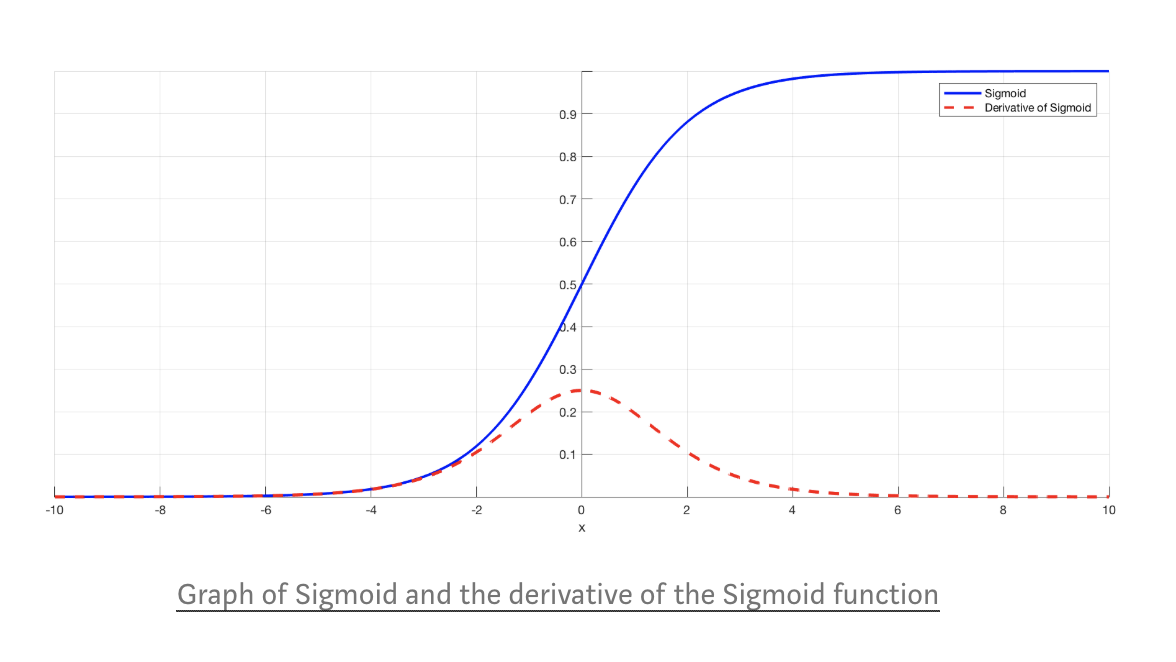
시그모이드는 입력값이 무엇이 들어오든 0~1 사이의 값으로 변환하기 때문에 확률과 이진분류에 활용이 가능

tanh 함수는 시그모이드와 유사하지만 출력값의 범위가 -1 ~ 1 이다.
미분된 형태를 보면 시그모이드 함수가 0 ~ 0.25인 것과 비교해 0~1의 넓은 범위 값을 가진다.
다중 레이어에서 시그모이드는 각 활성함수에 대한 미분을 여러 번 수행하면서 작아진 값을 또 미분하기 때문에
계속해서 작아지는 문제가 있었지만, tanh 함수의 경우에는 다중 레이어에서의 미분이 더 잘되어 경사하강이 잘 이루어짐
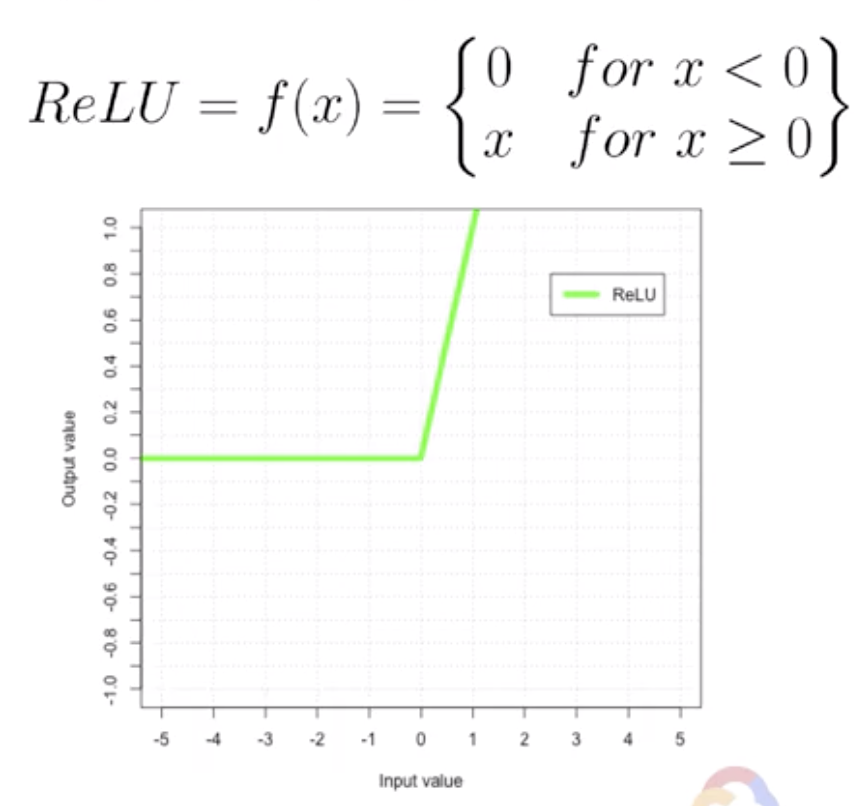
ReLU(Reflected Linear Unit)으로 입력값이 0 이하면 출력은 0, 입력값이 0이상이면 무조건 자신의 값이 출력이 되는 함수.
학습시 버릴 것은 확실히 버리고, 살릴 것은 확실히 살릴 수 있음.
살린 것에 대한 미분은 항상 1로 유지되어 학습이 잘됨.
하지만 버린 것에 대한 미분은 항상 0이어서 학습이 잘 되지 않음

ELU(Exponential Linear Unit)는 ReLU와 비슷하나 ReLU가 버리는 값에 대한 미분이 항상 0이어서 학습이 잘 안되던 문제를 보완.
이론적으로는 좋지만 e에 대한 계산이 복잡해서 컴퓨팅 자원이 많이 필요함
'구글 머신러닝 스터디잼(중급) > Launching into Machine Learning' 카테고리의 다른 글
| ML History 5 : Kernel Methods (0) | 2019.10.21 |
|---|---|
| ML History 4 : Decision Tree (0) | 2019.10.20 |
| ML History 2 : Perceptron (0) | 2019.10.18 |
| ML History 1 : Linear Regression (0) | 2019.10.18 |
| Supervised Learning 2 : Regression and Classification (0) | 2019.10.15 |